1、引言
在汽車結(jié)構(gòu)CAE分析中,模態(tài)分析、頻響分析和隨機(jī)響應(yīng)分析都是常見的分析項(xiàng),這些分析項(xiàng)在主機(jī)廠都是被劃分到NVH領(lǐng)域,而NVH工程師主要關(guān)心的是加速度和位移響應(yīng),不太關(guān)心應(yīng)力。所以文獻(xiàn)資料中對(duì)模態(tài)應(yīng)力、頻響應(yīng)力、和PSD應(yīng)力的介紹非常少。
近幾年來,基于道路譜的整車結(jié)構(gòu)疲勞分析已經(jīng)開始從準(zhǔn)靜態(tài)多通道法轉(zhuǎn)換到模態(tài)瞬態(tài)響應(yīng)法,頻域內(nèi)的強(qiáng)度和疲勞分析也已大量應(yīng)用。實(shí)施這些動(dòng)態(tài)的強(qiáng)度疲勞分析必然要涉及到上述三種應(yīng)力,所以我們有必要對(duì)模態(tài)應(yīng)力、頻響應(yīng)力和PSD應(yīng)力的概念做一些討論。
2、模態(tài)分析和模態(tài)應(yīng)力
我們通常說的模態(tài)指的是結(jié)構(gòu)的實(shí)模態(tài),其物理含義是,在沒有外界激勵(lì)和阻尼的條件下,結(jié)構(gòu)自身按特定頻率和特定的變形模式做簡諧振動(dòng),這個(gè)特寫頻率就是結(jié)構(gòu)的固有頻率,這種變形模式就叫做模態(tài)振型。
通過求解振動(dòng)特征方程,可以得到特征值與特征向量,即可得到相應(yīng)的固有頻率與模態(tài)振型。固有頻率和模態(tài)振型是結(jié)構(gòu)固有的一種屬性,它只與結(jié)構(gòu)的形狀、約束形式、材料特性等有關(guān),而與其他輸入(例如加載)無關(guān)。
模態(tài)振型是一種結(jié)構(gòu)變形模式,這種變形所對(duì)應(yīng)的應(yīng)力分布就叫做模態(tài)應(yīng)力。進(jìn)行模態(tài)分析時(shí),如果打開應(yīng)力結(jié)果輸出選項(xiàng),對(duì)應(yīng)每一階固有頻率,就有對(duì)應(yīng)的模態(tài)應(yīng)力結(jié)果輸出。模態(tài)應(yīng)力是相對(duì)應(yīng)力,和模態(tài)振型的相對(duì)概念是一樣的,它只表征結(jié)構(gòu)各點(diǎn)應(yīng)力的比例關(guān)系,其絕對(duì)數(shù)值并無意義。
模態(tài)振型和模態(tài)應(yīng)力的一些特征如下:
2.1 模態(tài)振型通過駐波描述,而這些駐波的節(jié)點(diǎn)位置是固定的,節(jié)點(diǎn)處的位移始終為0,但模態(tài)應(yīng)力通常不為0。
2.2 結(jié)構(gòu)上所有點(diǎn)在同一時(shí)刻,其位移分量和應(yīng)力分量達(dá)到****值或最小值。
2.3 結(jié)構(gòu)上所有點(diǎn)同一時(shí)刻通過零點(diǎn)位置,該時(shí)刻結(jié)構(gòu)的位移和應(yīng)力處處為0。
2.4 結(jié)構(gòu)上所有的點(diǎn),各位移分量和應(yīng)力分量要么完全同相位,要么完全反相位。
2.5無阻尼情況下計(jì)算得到的模態(tài)振型和模態(tài)應(yīng)力與比例阻尼情況下的模態(tài)振型和模態(tài)應(yīng)力相同。
3、頻響分析和頻響應(yīng)力
頻率響應(yīng)分析(簡稱頻響分析)用于計(jì)算結(jié)構(gòu)在正弦周期載荷作用下對(duì)每一個(gè)計(jì)算頻率點(diǎn)的動(dòng)態(tài)響應(yīng)。在頻率響應(yīng)分析中,激勵(lì)載荷是在頻域中明確定義的,載荷在每一個(gè)指定的頻率上都是已知的。計(jì)算的響應(yīng)結(jié)果為以實(shí)部和虛部形式表示的復(fù)數(shù),或由幅值和相位形式定義。
頻率響應(yīng)分析有兩類不同的數(shù)值方法可供選擇,即直接法和模態(tài)法。
直接法頻率響應(yīng)分析通過求解整個(gè)模型的阻尼耦合方程,得出結(jié)構(gòu)在一個(gè)穩(wěn)定的正弦周期外力作用下的響應(yīng)。結(jié)構(gòu)可以具有粘性阻尼和結(jié)構(gòu)阻尼,結(jié)果可輸出復(fù)位移、速度、加速度、約束力、單元力和單元應(yīng)力等。
模態(tài)法頻率響應(yīng)分析將結(jié)構(gòu)矩陣用忽略阻尼的實(shí)特征值分析進(jìn)行了壓縮,然后用模態(tài)坐標(biāo)建立廣義剛度和質(zhì)量矩陣。該分析的結(jié)果輸出類型與直接法相同。
在頻響分析中,如果我們設(shè)置單位正弦激勵(lì),針對(duì)某個(gè)頻段上的多個(gè)頻率點(diǎn)計(jì)算響應(yīng),其響應(yīng)結(jié)果就叫做頻響函數(shù)(以激勵(lì)頻率為橫坐標(biāo))。這個(gè)單位正弦激勵(lì)可以是力、力矩或壓力,也可以是位移、速度或者加速度。激勵(lì)的單位也不局限于國際單位制,比如單位加速度激勵(lì),可以用1.0m/s2的加速度,也可以用1.0g的加速度,當(dāng)然最后計(jì)算得出的頻響函數(shù)的含義也不相同。
頻響函數(shù)表征了線性系統(tǒng)在給定頻率下的穩(wěn)態(tài)輸出與輸入的關(guān)系。這個(gè)關(guān)系具體是指輸出輸入的幅值之比與激勵(lì)頻率的函數(shù)關(guān)系,和輸出輸入的相位差與激勵(lì)頻率的函數(shù)關(guān)系。這兩個(gè)關(guān)系稱為線性系統(tǒng)的頻響特性。頻率響應(yīng)函數(shù)是復(fù)函數(shù),可分解為幅頻特性曲線和相頻特性曲線分別研究。
如果我們研究的系統(tǒng)響應(yīng)為結(jié)構(gòu)應(yīng)力,則此時(shí)的頻響函數(shù)叫做應(yīng)力頻響函數(shù),也叫作頻響應(yīng)力。頻響應(yīng)力表征的是單位正弦激勵(lì)下的應(yīng)力張量響應(yīng),它包含了各應(yīng)力分量的頻率響應(yīng)曲線。通常我們更關(guān)心這些應(yīng)力分量的合成效果,即Von Mises應(yīng)力的頻響曲線。頻響應(yīng)力曲線的峰值點(diǎn)一般是對(duì)應(yīng)著結(jié)構(gòu)的某階固有頻率。
圖1展示了某電池包分別承受X、Y和Z向加速度激勵(lì)時(shí),殼體上某點(diǎn)的Von Mises應(yīng)力頻響曲線。
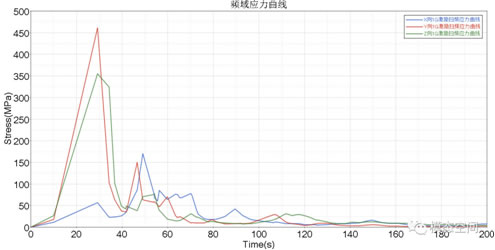
圖1 結(jié)構(gòu)上某點(diǎn)von Mises應(yīng)力的頻響曲線
在計(jì)算頻響應(yīng)力時(shí),應(yīng)設(shè)置符合實(shí)際情況的阻尼。如果沒有具體試驗(yàn)測試數(shù)據(jù),對(duì)于汽車車身結(jié)構(gòu)而言,建議模態(tài)阻尼(臨界阻尼系數(shù),即Nastran中CRIT形式)設(shè)置為0.02。
需要注意的是,由于阻尼的存在,結(jié)構(gòu)各點(diǎn)的頻響應(yīng)力可能相位不同,甚至同一點(diǎn)的各應(yīng)力分量的頻率響應(yīng)函數(shù)也可能相位不同,這點(diǎn)與模態(tài)應(yīng)力有很大差異。
計(jì)算頻響應(yīng)力時(shí),頻率點(diǎn)的間隔需要仔細(xì)斟酌,如果頻率點(diǎn)取得太稀疏,那么很可能漏掉應(yīng)力頻響曲線的峰值點(diǎn),導(dǎo)致后續(xù)強(qiáng)度和疲勞分析的結(jié)果過于激進(jìn)。頻率點(diǎn)如果取得太密集,固然可以提升分析精度,但在每一個(gè)頻率點(diǎn)都輸出結(jié)構(gòu)的全場應(yīng)力,我們將得到一個(gè)龐大的頻響應(yīng)力結(jié)果文件,很可能導(dǎo)致強(qiáng)度和疲勞分析軟件無法處理。比較好的方案是在結(jié)構(gòu)的各階固有頻率附近采用密集的頻率點(diǎn),在各階固有頻率之間采用稀疏分布的頻率點(diǎn)。
圖2和圖3分別展示了使用Nastran和Abaqus計(jì)算頻響應(yīng)力的頭文件,結(jié)構(gòu)所受的載荷為加速度激勵(lì)。

圖2 計(jì)算頻響應(yīng)力的Nastran頭文件

圖3 計(jì)算頻響應(yīng)力的Abaqus頭文件
采用模態(tài)法計(jì)算結(jié)構(gòu)頻響應(yīng)力,首先將結(jié)構(gòu)動(dòng)力學(xué)方程進(jìn)行模態(tài)解耦,然后針對(duì)解耦的各單自由度系統(tǒng)求得模態(tài)坐標(biāo)的頻響函數(shù),

其中Hi(ω)為第i階模態(tài)坐標(biāo)的頻率響應(yīng)函數(shù),Pi、mi、bi和ki分別為第i階模態(tài)力、模態(tài)質(zhì)量、模態(tài)阻尼和模態(tài)剛度。
頻響應(yīng)力則由各階模態(tài)坐標(biāo)的頻響函數(shù)和對(duì)應(yīng)的模態(tài)應(yīng)力相乘疊加得到,
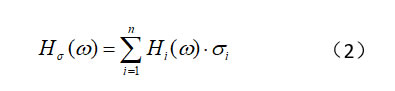
其中Hσ(ω)為頻響應(yīng)力,σi為第i階模態(tài)應(yīng)力。
按照這個(gè)思路,我們可以不直接計(jì)算輸出頻響應(yīng)力結(jié)果,而是先通過一個(gè)實(shí)模態(tài)分析輸出各階模態(tài)應(yīng)力σi,這個(gè)結(jié)果文件的大小取決于模態(tài)分解的階數(shù);再通過一個(gè)模態(tài)法頻響分析輸出各階模態(tài)坐標(biāo)的頻響函數(shù)Hi(ω),這個(gè)結(jié)果文件只包含了一些單自由度系統(tǒng)的頻響曲線,所以其大小通常不過幾兆字節(jié)。在進(jìn)行后續(xù)強(qiáng)度或疲勞分析時(shí),頻響應(yīng)力再利用公式(2)得出。
這樣做的好處是,我們即使將頻率點(diǎn)設(shè)置的非常密集,模態(tài)坐標(biāo)頻響函數(shù)結(jié)果文件也只會(huì)增大幾兆字節(jié),模態(tài)應(yīng)力結(jié)果文件的大小則不會(huì)改變。從而在控制結(jié)果文件大小的同時(shí),避免了遺漏頻響應(yīng)力曲線上的峰值點(diǎn),特別適合模型規(guī)模大且激勵(lì)頻帶很寬的情況。
4、隨機(jī)響應(yīng)分析與PSD應(yīng)力
隨機(jī)響應(yīng)分析用于計(jì)算結(jié)構(gòu)在隨機(jī)激勵(lì)載荷作用下的響應(yīng)。隨機(jī)激勵(lì)載荷是頻域信號(hào)表征的,通常采用功率譜密度函數(shù)(PSD)表示。隨機(jī)激勵(lì)下的響應(yīng)是統(tǒng)計(jì)意義下描述的響應(yīng),在任何瞬時(shí)響應(yīng)具體大小未知,但其大小的概率可以給出。
隨機(jī)響應(yīng)分析通常是作為頻率響應(yīng)分析的后處理。首先施加單位正弦激勵(lì),得到頻響函數(shù),然后根據(jù)用戶給定的載荷條件(形式為各載荷的自功率譜密度和互功率譜密度)。輸出為響應(yīng)的功率譜密度、響應(yīng)的自相關(guān)函數(shù)或響應(yīng)的均方值,其中應(yīng)力響應(yīng)的功率譜密度我們簡稱為PSD應(yīng)力。
與頻響函數(shù)一樣,響應(yīng)的PSD也是以頻率為橫坐標(biāo)的函數(shù),但PSD是正的實(shí)函數(shù),并沒有相位的概念。
一個(gè)線性系統(tǒng),承受平穩(wěn)隨機(jī)激勵(lì)載荷x(t),其PSD為Sx(ω),響應(yīng)信號(hào)為y(t),其PSD為Sy(ω),則可按下式計(jì)算y(t)的功率譜密度,
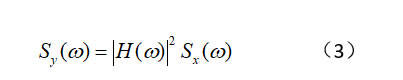
其中H(ω)為載荷x(t)所對(duì)應(yīng)的頻響函數(shù)。
如果有多個(gè)隨機(jī)載荷信號(hào)x1(t),x2(t),…,xN(t)共同作用,則
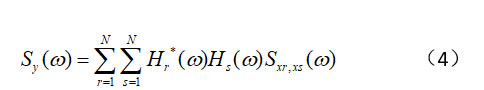
其中Sxr,xs(ω)當(dāng)r≠s時(shí),為載荷xr(t)和xs(t)的互功率譜密度函數(shù)(CPSD);當(dāng)r=s時(shí),為載荷xr(t)的功率譜密度函數(shù)。
對(duì)于互不相關(guān)的多個(gè)載荷信號(hào),其互功率譜密度全部為零,則
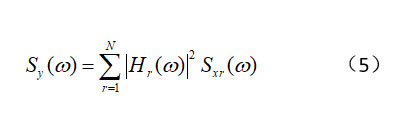
所以,只要有各載荷的頻響函數(shù)Hr(ω),我們就可以根據(jù)激勵(lì)載荷的PSD矩陣來求得結(jié)構(gòu)上各點(diǎn)的PSD應(yīng)力。圖4展示了一個(gè)卡車車身的載荷PSD矩陣,,共有12個(gè)載荷通道,構(gòu)成12*12的PSD矩陣,其中對(duì)角項(xiàng)為各載荷的自功率譜密度函數(shù),非對(duì)角項(xiàng)為互功率譜密度函數(shù)。
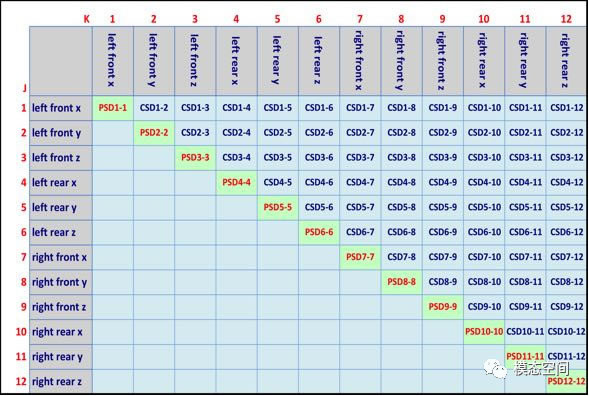
圖4 隨機(jī)激勵(lì)載荷的PSD矩陣
PSD應(yīng)力表征的是隨機(jī)激勵(lì)下的應(yīng)力張量響應(yīng),它包含了各應(yīng)力分量的PSD曲線。得到PSD應(yīng)力后,再依據(jù)某些頻域疲勞失效模型,例如Dirlik算法、Lalanne算法或Steinberg算法等,就可以得到應(yīng)力幅值區(qū)間的概率分布,進(jìn)而得到疲勞壽命或者損傷值。
5、隨機(jī)激勵(lì)下Von Mises應(yīng)力的有效值
對(duì)于平穩(wěn)隨機(jī)過程,響應(yīng)信號(hào)的均方根值,即有效值(RMS),可以由其PSD在頻域內(nèi)積分得到,即
這是功率譜密度函數(shù)Sy(ω)最重要的一個(gè)特性,即功率譜密度曲線下的面積就是平穩(wěn)隨機(jī)過程y(t)的功率E(y2),即均方值,如圖5。功率E(y2)開平方后就是y(t)的有效值。
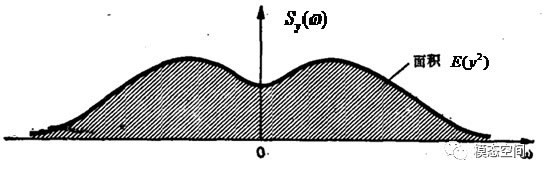
圖5 功率譜密度曲線與均方值
所以只要我們通過隨機(jī)響應(yīng)分析計(jì)算得到PSD應(yīng)力后,各應(yīng)力分量的均方根值都可以用上式得到。
我們通常不太關(guān)心各應(yīng)力分量的均方根,而是關(guān)心Von Mises應(yīng)力的均方根。對(duì)于汽車上的鈑金結(jié)構(gòu),有一種估算疲勞壽命的簡單方法:如果隨機(jī)載荷引起的結(jié)構(gòu)上各點(diǎn)Von Mises應(yīng)力的均方根值小于材料拉伸極限的20%,基本可以認(rèn)為能達(dá)到無限疲勞壽命。
引用.汽車測試網(wǎng) https://www.auto-testing.net/news/show-99799.html
以上內(nèi)容由應(yīng)變儀生產(chǎn)廠家-江蘇泰斯特(http://www.fengnew.com/)與你分享,若有謬誤,敬請指正。

